¿Cuánto le debe Pixar al asteroide Ceres?
Publicado: el 10 mayo, 2023 por / Konrad Lorenz

Figura 1. Personaje “Turning red”
Está claro que los avances científicos tienen gran repercusión en todos los aspectos de nuestra vida, entre ellos, el entretenimiento. Un ejemplo claro de esto es el cine, pasando por los proyectores, dispositivos de sonido e incluso, nuestro propio televisor. Todo esto ha sido fruto de años de trasegar científico. En este orden de ideas, ¿Qué tiene que ver un asteroide descubierto en 1801 con Mei Lee de Turning red o Woody de Toy story?
Por sorprendente que parezca, hay un camino que une dicho asteroide con los personajes animados de Pixar. Todo empieza con un famoso matemático llamado Carl Gauss quien solucionó el problema del asteroide perdido, ya que sus contemporáneos divisaron un asteroide que luego desapareció; fue el joven Gauss el que indicó a dónde apuntar los telescopios, ¿cómo lo hizo? descifró su trayectoria.

Figura 2. Trayectoria de un asteroide
El descubrimiento del matemático aportaría a la ciencia métodos y conceptos usados hasta hoy, además, catapultarían aún más la fama del joven. El método de eliminación Gaussiana, aunque no fue su más remarcable aporte, tuvo una importancia fundamental para futuros desarrollos y muchos años después, para la creación de personajes en tres dimensiones.
La batuta dejada por Gauss fue tomada por Arthur Cayley y Joseph Silvester, el primero, introduce el concepto de matriz, partiendo de sistemas de ecuaciones lineales, Silvester por su parte, acuña el término de matriz como tal, operaciones entre ellas y otros conceptos fundamentales como la matriz identidad.
Frente a lo anterior surge la pregunta: ¿Qué tienen que ver las matrices con los personajes de Pixar? si bien, aún faltan muchos años para su uso, la modelación de personajes y escenarios, tanto animados como estáticos, se basan en matrices y en los nodos que se generan en las intersecciones.

Figura 3. Matriz y forma 3D
Partiendo de los avances con las matrices, en la última década del siglo XIX nace la Teoría Espectral de Matrices, en donde, entre muchas otras cosas, se clasifican las matrices y se fundan las bases para que Pears tiempo después, pueda definir el Álgebra Finito Dimensional, dando paso a los espacios vectoriales y el producto entre sí.
Los personajes animados o mejor dicho, las líneas que los componen, viven en un espacio de tres dimensiones, de allí su famoso nombre de animaciones 3D, similar a lo mostrado en le figura 3, trabajar en estos espacios no habría sido posible sin la teoría antes descrita.
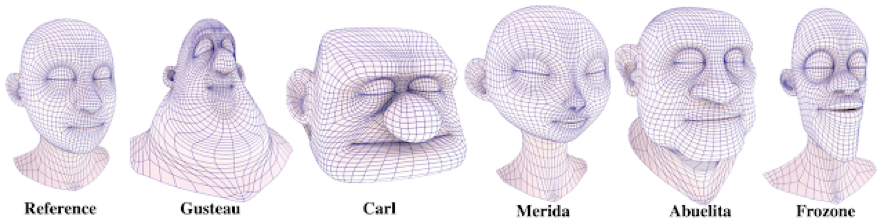
Figura 4. Malla de referencia y malla de figura de personajes Pixar
Grassman y Peano ampliaran el trabajo con espacios vectoriales, el último aportando la definición de los mismos y Grassman, por su parte, aporta uno de los conceptos más claves del álgebra lineal y del tema que nos concierne en este artículo: Las transformaciones lineales, mediante las cuales se puede transportar, rotar y en general modificar los vectores de un espacio, que, en este caso, son líneas que forman una forma, como se muestra en la figura 4.
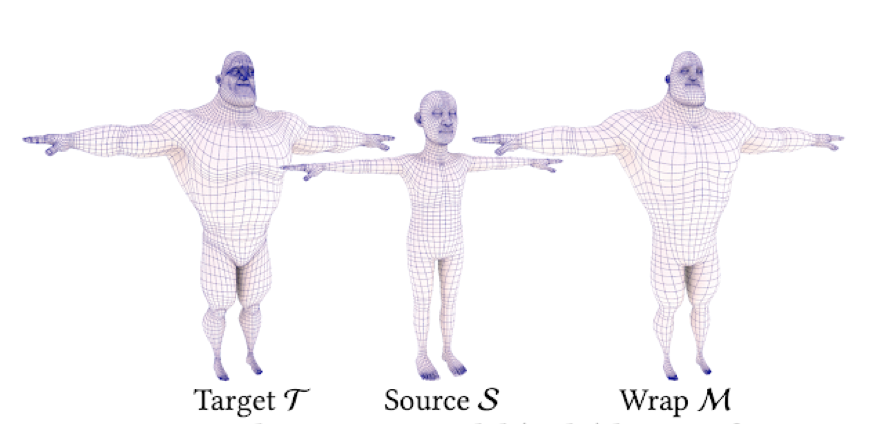
Figura 5. Transformación lineal Wrap
Finalmente, el software usado por los animadores de Pixar toma una malla o matriz de referencia (S), cómo se ve en la figura 5, a la que se le aplicará una transformación lineal (M) que es llamada como Wrap, ya que lo que consigue es envolver la referencia y transformarla en el objetivo final (T), que en el caso de la figura 5 es Mr. Increíble.
Este camino recorrido que abarca muchos años, termina en la sofisticada implementación de conceptos y teorías algebraicas en la animación en tres dimensiones. Sin embargo, no deja de ser curioso cómo todo empezó con un asteroide perdido en el espacio y un joven matemático que se atrevió a calcular su trayectoria.

Figura 6. Personaje Turning red en movimiento
Referencias
– Ferre Vaccarezza, E; Le Cleinche, S. (2019). Un paseo por los espacios n-dimensionales. Madrid: Prisanoricias Colecciones
– De Goes, F., & Martinez, A. (2019). Mesh wrap based on affine-invariant coordinates. ACM SIGGRAPH 2019 Talks. recuperado en: https://graphics.pixar.com/library/WrapperSIGGRAPH2019/paper.pdf
– De Goes, F., Shuffler, W., & Fleischer, K. (2022). Character articulation through profile curves. ACM Transactions on Graphics, 41(4), 1–14. https://doi.org/10.1145/3528223.3530060
Juan Sebastián Vargas Arévalo
Estudiante de Matemáticas
Tercer semestre
27 de abril de 2023




