Ecuación de Black – Scholes. La importancia de las matemáticas en el desarrollo económico

Este modelo matemático puede ser uno de los implicados en la gran catástrofe económica del 2008-2009 donde se presentó una enorme burbuja inmobiliaria junto a una crisis de liquidez, por lo cual surge el siguiente cuestionamiento: ¿Qué importancia tienen las Matemáticas dentro del sector financiero y por consiguiente en la economía mundial?

En 1973, Robert Merton publica el escrito denominado “ Theory of Rational Option Pricing ” en donde mencionó por primera vez, el modelo matemático desarrollado por Fisher Black y Myron Scholes para estimar el precio de opciones financieras, siendo esto una gran ayuda para todo aquel que trabajara en el mercado bursátil.

Dentro del campo de la matemática financiera, la Ecuación de Black – Scholes es un poderoso instrumento para calcular el precio de determinados activos financieros, concretamente los productos conocidos como derivados.

En primer lugar, definiremos el concepto del instrumento financiero conocido como derivado, el cual es un acuerdo de compra o venta de un activo determinado, con una fecha futura ya pactada y con un precio establecido. ¿Sobre qué título de inversión se fija este acuerdo? En general, este trato se establece sobre activos subyacentes tales como acciones, títulos de renta fija, divisas, entre otros, por lo cual el modelo ha sido ampliamente utilizado en las bolsas de valores a nivel mundial.

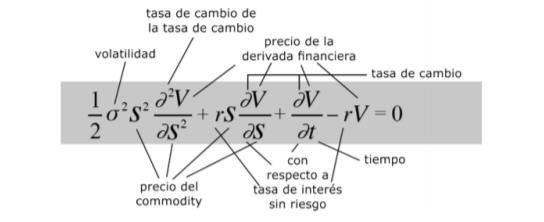
Ahora, veremos a grandes rasgos, la famosa ecuación que generó un masivo crecimiento del sector financiero y posteriormente las crisis financieras del 2008 y 2009 junto a una fuerte depresión económica:

Imagen 1. Ecuación de Black – Scholes. 17 ecuaciones que cambiaron el mundo (p. 338). Stewart. I. 2013. España: Grupo Drakontos

Cuando una persona o compañía invierte en el mercado de capitales, siempre aparece un factor muy influyente: la volatilidad de las inversiones, ya que dependiendo del tipo de inversión que quiera realizar un sujeto, este debe tener muy claro en dónde coloca sus recursos y que riesgo conlleva dicha acción.

Este modelo matemático, usa diversos criterios estadísticos, como por ejemplo la campana de Gauss, la desviación estándar, conceptos probabilísticos, entre otros. Dichos conceptos se utilizan con el fin de lograr determinar a qué valor y con qué riesgo se cuenta a la hora de comprar o vender derivados. Curiosamente los encargados de hacer las evaluaciones y construcciones de las posibles fluctuaciones en el mercado eran generalmente estadísticos, físicos o matemáticos.

Cuando las entidades financieras y de inversión se dieron cuenta del potencial matemático para construir modelos de predicción con gran exactitud y altas ganancias, el modelo de Black – Scholes entró a jugar un rol fundamental en el crecimiento de transacciones en el mercado, dando una pauta para colocar precio a un derivado, teniendo en cuenta una serie de suposiciones lógicas del entorno junto a cinco parámetros descritos a continuación:

t = tiempo
S = Precio del producto
V = Precio del derivado
r = Tasa de interés de riesgo
?² (Sigma) = volatilidad de las acciones

Para una mejor comprensión de este modelo, Stewart (2013) afirma que: “Expresa la Tasa de variación del precio del derivado respecto con el tiempo, como una combinación lineal de tres términos: el precio propio del derivado, lo rápido que cambia en relación al precio de la acción y cómo ese cambio acelera” (p. 347).

En el mercado de valores, existen las opciones de compra y las de venta, cada una con una estructura especial para calcular el valor recomendado para negociar el derivado, dando así cierta base racional y teórica a las negociaciones hechas en la bolsa. Ahora, vamos a colocar un ejemplo breve para dimensionar la importancia de este modelo matemático:

Supongamos que hemos comprado Bonos emitidos por parte del Gobierno colombiano. Para contextualizar, los Bonos son títulos de deuda, con el fin de obtener financiamiento para proyectos establecidos a un plazo determinado. El emisor (en nuestro caso el Gobierno Colombiano), se compromete a devolver el capital prestado junto a los intereses, en un período pactado. Dicho título se comercializa en las Bolsas de valores. Imaginemos también, que el Bono tiene fecha de vencimiento a diciembre de 2020, pero lo queremos vender antes de dicha fecha.

La pregunta que surge ahora es: ¿cómo puedo saber a qué precio debo vender o comprar la opción de este título de inversión?

La respuesta se encuentra en la utilización del ingenioso modelo de Black – Scholes para tener certeza de no perder dinero, ya que en el mercado financiero se juegan con cifras monetarias exorbitantes. La efectividad del modelo se adapta al comportamiento del mercado y fue tan buena que hizo que Merton y Scholes ganaran el Nobel de Economía en 1997. Black ya había muerto para ese momento.

Debido a la confianza sobre este modelo matemático junto a la libertad de mercado, las compañías financieras comenzaron a ignorar los pequeños detalles que mostraba el sistema en ciertos momentos históricos como la crisis económica de Rusia por la caída de precios del petróleo, generando así varias inconsistencias. Un ejemplo claro es la compañía Long Term Capital Management, quien hasta 1998 generó unas ganancias del 40% anual pero luego, en menos de cuatro meses, tuvo pérdidas por 4.600 millones de dólares, cerrando finalmente la compañía en el 2000. Otro caso es Enron, compañía energética que en 2001 quebró y causó uno de las mayores bancarrotas en Estados Unidos, cuya pérdida para los accionistas fue por 11.000 millones dólares, mostrando de nuevo la poca regulación hecha por entes gubernamentales a los mercados junto al mal manejo de los modelos matemáticos y el poco sentido ético de las compañías involucradas.

Por último podemos concluir qué impacto puede lograr la matemática aplicada al mundo real, cabe resaltar que este impacto siempre será favorable para todos, siempre y cuando se logre interpretar, analizar y aplicar de manera adecuada los conceptos del análisis matemático que tiene el planteamiento de cualquier problema.

Michael Andrés Mora Poveda

Estudiante de Matemáticas

Referencias:
1) Bolsa de valores de Colombia. (2017). Derivados. Bogotá, Colombia. Recuperado de http://www.tradersbvc.com.co/derivados
2) Stewart. I. (2013). 17 Ecuaciones que cambiaron el mundo. España, Drakontos.